中学生になり、数学の角度でつまずいているあなた、こんな悩みはないでしょうか?
・教科書の説明が分かりにくい
・問題がスラスラ解けない
・答えを見れば理解はできるのに…
中学生の数学で角度に自信のない方は多いと思います。
「錯角がどこかなんて知らないよ!」という方もいるでしょう。
安心してください。
この記事を読み終わるころには、問題でつまることなく、スラスラ解けるようになります。
ではやっていきましょう!
角度の基本を押さえよう
角度の問題を解くうえで、知らなければいけないことがいくつかあります。
一つずつやっていきましょう。
①対頂角
角度関係の暗記ができない方は、今からいうことをよく覚えておいてください。
角の場所は、漢字を見ればわかります。
まずは対頂角です。
漢字の通りに解釈していきましょう。
「対」という感じは、Aチーム対Bチームのように使いますよね。
このことからわかるように、「対」には向かい合うという意味があります。
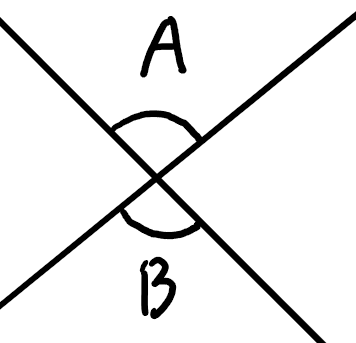
上の図からもわかるように、対頂角は「向かい合う角」のことをいうのです。
②同位角、錯角
対頂角と同じように考えます。
同位角を分かりやすく言うと「同じ側にある角」です。
「位」というのは方位など、方向を表しますよね。
次に錯覚です。
「錯」という字が今回覚えることの中で1番イメージしにくいかもしれないです。
「錯」という字を辞書で調べると「交ざる、入り乱れる」と出てきます。
イメージとしては図で考えましょう。
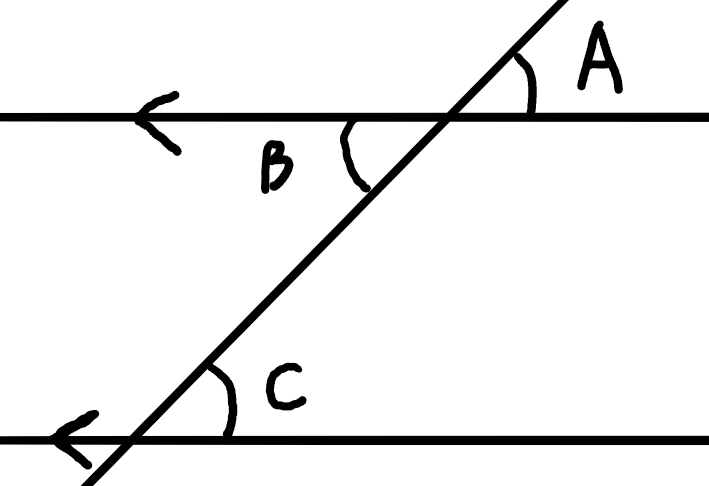
角Aと角Cは「同じ側」にあるので、同位角です。
次に、角Bと角Cを見てみましょう。
交差しているのが分かりますね。
角B角Cの関係が錯覚です。
ちなみに角Aと角Bの関係は分かりますか?
答えられなかった人は少し前に戻ってみてください。
(答えは対頂角です)
③平行線と角
同位角と錯覚が問題に出てくるときに、ほぼ確実にセットで出てくるのが平行線です。
平行ってなんだっけ?という方のために説明します。
平行とは、どこまで線を伸ばしても交わらないということです。
図にしてみましょう。
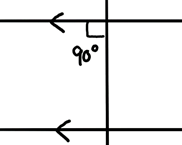
2つの直線が平行であるということは、線上にある<のマークで表されることが多いです。
平行な2つの直線があるとき、片方に垂直な線を引くと、もう片方にも垂直になるということもおさえておくと、今後良いことがあるかもしれません。
平行線と同位角、錯角がセットになった場合を考えてみましょう。
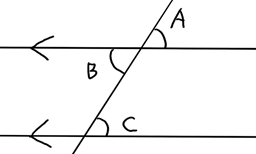
この時のそれぞれの角の関係を確認していきましょう。
まずは、角Aと角B。
向かい合っているので、対頂角ですね。
よって、角A=角B
次に、角Aと角Cです。
同じ側にあるので、同位角です。
角Bと角Cは交差しているので、錯角です。
これで、終わってはいけません。
上の図の2つの直線は平行です。
このとき、同位角である角Aと角Cについて、角A=角Cが成り立ちます。
錯角も同じく、等しくなるので、角B=角Cとなります。
平行線がセットとなった時の同位角、錯角の性質を覚えておきましょう。
④多角形の内角
多角形とは、その名の通り「多くの角がある図形」です。
これは公式があるので、まずは見てみましょう。
多角形の内角の和=180×(角の数-2)
「暗記だ…。」と中学生の僕は思いました。
しかし、この記事では暗記で終わらせません。
図で「理解」していきましょう。
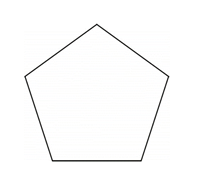
正五角形があります
この図形に線を付け足して考えやすくしてみます。
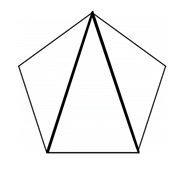
この時のポイントは、1つの頂点からできるだけ多く対角線を引くことです。
図形を見て、分かることは何でしょう?
三角形が3つあるということです。
ここで、三角形の内角の和は180度であることを思い出します。
すると、五角形の内角の和は180×3=540で
540度であることが分かります。
公式に戻りましょう。
多角形の内角の和=180×(角の数-2)
どうですか?
公式に当てはまっていますね。
今回紹介した公式は、多角形の中にある三角形の数を数えるためのものだったことが分かります。
この考えを使えば、どの多角形の内角の和も計算できるなんて最高ですよね。
⑤補助線の引き方
④の説明の中で「線を付け加える」ということをしました。
これが、補助線というものです。
補助線というのは、問題を考えやすくするために引くものです。
応用問題にはよく出る考えなので、「補助線」という言葉を覚えておきましょう。
また、補助線を引くときに大切なことを一つだけ教えておきます。
それは、「知っているものを使うために引く」ということです。
④では、すでに知っている三角形の内角の和を使うために補助線を引きました。
この考えを頭の片隅に置いておいてください。
練習問題を解いてみよう
ではさっそく、上記のことを使って問題を解いてみましょう!
問題
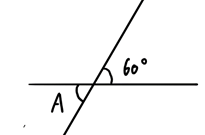
(1)角Aの角度を求めよ。
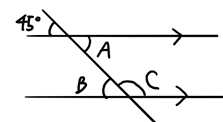
(2)角A、角B、角Cそれぞれの角度を求めよ。
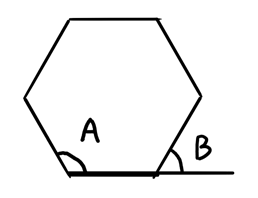
(3)正六角形がある。角A、角Bの角度を求めよ。
解答
(1)A=60度
対頂角の問題です。対頂角の性質を使いましょう。
(2)A=45度、B=45度、C=135度
まずは、対頂角の性質を使い、A=45度と分かります。
次に、平行線に着目します。
角Aと角Bは錯角の関係にあるので、B=45度です。
同位角の性質を使って、角Bを求めることもできますね。
角Bが求められたら、C=180-45で求められますね。
(3)A=120度、B=60度
まずは、角Aを求めます。
多角形の内角の和の求め方を覚えていますか?
忘れてしまった方は、上の説明で仕組みを「理解」してから戻ってきてください。
式に当てはめると、内角の和は720度と分かります。
正六角形なので、すべての角は等しく、A=120度と分かります。
B=180-120で60度ですね。
まとめ
いかがだったでしょうか。
角度は応用までずっとついてきます。
まずは、基本となることを押さえてスピード感を持って問題を解けるようにしていきましょう。








