「解の公式を書いてみて!」と言われて、すぐに書けますか?
中学生の習う数学で、点数を稼ぐために最も大事なことは「公式を覚えること」です。
どんなに数学が苦手な人でも、公式を覚えていれば必ず点が取れます。
さらに、公式を理解していれば数学が得意教科になっていくでしょう。
この記事では、テストや模擬試験の直前に見直しておきたい公式をおさらいしていきます。
この記事で紹介する公式を復習しておけば
「公式忘れてた…。」
という悲しい事件を減らせると思います。
中学数学での公式
正直、私は公式を丸暗記するのはおすすめしていません。
なぜなら、公式を暗記するだけでは応用問題に対応できない場合があるからです。
さらに、丸暗記した公式は記憶から抜け落ちやすいです。
しかし、理解をしなくとも取れる問題は増えます。
また、理解をするより覚えてしまった方が早いものもあります。
今回は、暗記をしてしまう方がよい公式を紹介していきます。
覚え方などは紹介しますが、時間があるときに、ぜひ自分で理解するようにしてみてください。
乗法公式
①(x+a)(x+b)=x²+(a+b)x+ab
②(a+b)²=a²+2ab+b²
③(a−b)²=a²−2ab+b²
④(a+b)(a−b)=a²−b²
①(x+a)(x+b)=x²+(a+b)x+ab
xの部分が同じ文字であることがポイントです。
先頭どうしをかける→後ろを足して先頭をかける→後ろどうしをかけるという手順です。
分配法則が分かっていれば、それでも良いと思います。
②(a+b)²=a²+2ab+b²、③(a−b)²=a²−2ab+b²
2つある文字をどちらも二乗する→2×2つの文字(符号も入れて考える)です。
これも分配法則が使えます。
④(a+b)(a−b)=a²−b²
文字の+、-のかけ算がでてきたら、前の2乗-後ろの2乗です。
なお、分配法則は使えます。
円と扇形
半径がrの円があるとき
面積:πr²
円周の長さ:2πr
中心角がa度の扇形は、上の式にそれぞれa/360をしてあげればOKです。
円錐
中心角:半径/母線×360(母線は円錐の先端に向かう辺のことです)
側面積:母線×半径×中心角/360
円錐の問題に当たったら、図形を展開しましょう。
立体で考えるのではなく、平面で考えた方が全体をとらえやすいです。
球
表面積:4πr²
体積:4/3πr³
球の公式は覚えにくいですが、4という数字を覚えておくと少し楽になります。
語呂合わせで覚えたい方は、「表面は心配あるある」、「身の上に心配あーる三乗」というものがあるので、公式と照らし合わせて覚えるとよいと思います。
合同と相似
合同条件:①3辺がそれぞれ等しい
②2辺とその間の角が等しい
③1辺とその両端の角が等しい
相似条件:①3つの辺がそれぞれ等しい
②2辺とその間の角がそれぞれ等しい
③2組の角がそれぞれ等しい
この条件を丸暗記している人にありがちなこととして、合同な図形は相似でもあるということを知らない、ということがあります。
相似は形が同じで、大きさが異なる図形のことをいいます。
このことを覚えておくと、条件を忘れてしまっても、思い出しやすくなると思います。
平行四辺形の条件
①2組の対辺がそれぞれ平行(定義)
②2組の対辺がどちらも等しい
③2組の対角がどちらも等しい
④対角線がそれぞれの中点で交差
⑤1組の対辺が平行かつその長さが等しい
中点連結定理
△ABCにおいて、辺ABと辺ACの中点をそれぞれ、M、NとするとMN//BCであり、MN=1/2BCである。
これは、中点ということがポイントとなります。
中点という名前が出てきたら、この公式を思い浮かべましょう。
相似比
2つの相似な三角形があり、その相似比がA:Bの時、2つの三角形の面積比はA²:B²であり、体積比はA³:B³である。
まずは、相似な三角形の対応する辺を探しましょう。
円周角
円周角の定理として知っておいてほしいことは
①弧の長さが同じなら、中心角も円周角も等しい
②同じ弧に対する中心角は円周角の2倍である
③直径に対する円周角は90度になる
④円に内接する四角形の向かい合う角の和は180度である
細かく書くとほかにもいくつか覚えることはあるのですが、この4つを覚えておけばすべておさえられます。
弧の長さと円周角の大きさは比例するということがポイントです。
接弦
今までの公式はできるだけ文字で説明してきました。
これは、すべての公式を視覚的に覚えると、交ざって覚えてしまうからです。
しかし、この公式は視覚的に覚えた方が圧倒的に早いので、図で説明します。
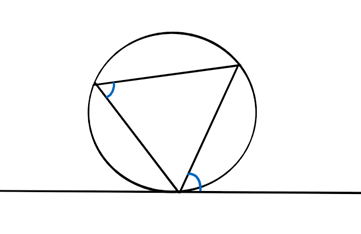
円と円に接している線があり、接点を頂点とする三角形があるとき、青い角は等しい
角の配置を視覚的に覚えるのが手っ取り早いと思います。
忘れやすいので、時間があるときに証明を見ておくとよいと思います。
三平方の定理
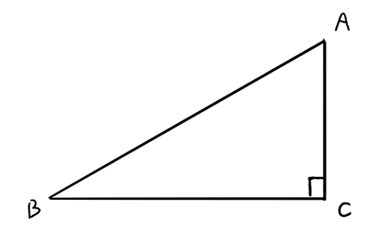
角Cが90度の直角三角形があるとき、辺AB、辺BC、辺CAついて
AB²=BC²+CA²という関係が成り立つ。
三平方の定理は、本当によく使うので必ず覚えましょう!
また、直角三角形のうち、下に載せておいた2つの代表的なものは辺の比を覚えておくと、計算が早くなります。
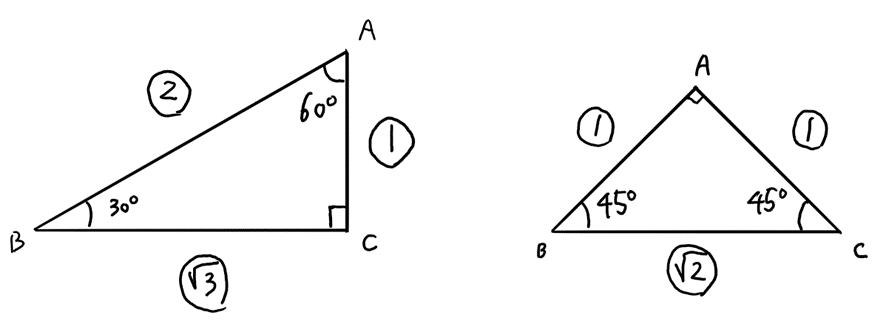
二次関数の裏技
y=ax² という二次関数があり、x が p から q まで変化するとき
y=ax² の変化の割合はa(p+q)
と表せます。
また、切片(y切片)は-apqで表せます。
この二つの公式は、条件がそろわないと使えません。
しかし、条件がそろえば一撃必殺として使うことができます。
他の公式を覚えていて、余裕のある方だけ覚えてください。
まとめ
中学生の数学では、覚えてしまった方が早い公式というものが結構ありますし、知らないと解けない問題が多いです。
テスト前に確認している方、後でもう一度見てください。
勉強の途中で見ている方、できるだけどうして公式が成り立つのか、疑問を持ってください。
それが一番記憶に残る方法です。







