相似って面倒くさいという印象が強いと思います。
「条件を覚えられない」「合同との違いが分からない」
それぞれの感想があると思います。
この記事では、相似をかみ砕いて説明しています。
読み終わるころには、相似のイメージがはっきりし、問題も解けるようになります。
ぜひ、最後までお読みください!
相似の条件
「相似」というのは漢字にもある通り、「似ている」図形のことを言います。
ずばり、似ているのは、形ですね。
大きさは関係ありません。
イメージとしては下のような感じです。
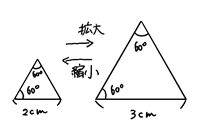
簡単に言えば、拡大と縮小の関係なのです。
少しつかめたでしょうか?
三角形について「相似」と言える条件を見ていきます。
3つの辺の比がすべて等しい
まず、「辺の比」という言葉が引っかかるかもしれませんね。
具体的に考えてみましょう。
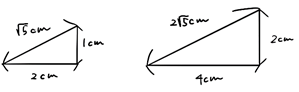
上の2つの三角形の大きさは違いますが、3つの辺の比は同じです。
拡大と縮小の関係になっているのです。
では、3つの辺の比が同じだと、どうして同じ形になるのでしょう?
それは、3つの辺の比が同じである2つの三角形は対応する角の大きさがすべて等しいからです。
最初のイメージの画像を思い出しましょう。辺の長さが変わっても角度は変わっていませんよね。
これが相似で大切なことです。
2つの角が等しい
これは、先ほど説明したことが分かれば、すぐ理解できます。
3つの辺の比がすべて等しい=対応する角の大きさが等しい
先ほどやりましたね。
今度は2つの角が等しければ、相似となるようです。
勘の良い方は気づいていると思いますが、三角形は角が3つしかありません。
その中の2つが同じということは…。
そう、すべての角が等しいと言っているのと同じなのです。
根本の考えは同じだったということが分かりますね。
2組の辺の比と、その間の角がそれぞれ等しい
この条件は図にしてみると分かりやすいです。
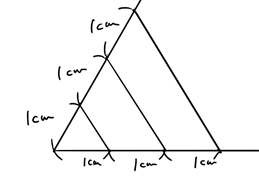
3つの三角形が見えると思います。
一つの角は共有しているので、等しいですね。
辺の長さは小さい三角形から1㎝、2㎝、3㎝です。
これもまた、拡大と縮小の関係ですね。
言葉を覚えよう
1度理解できたら、言葉を覚えましょう。
本番で使うのは、残念ながら決められた言葉ですので…。
中点連結定理
これも良く問題に出てきますね。
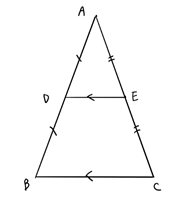
式で表すと、AE=EC,AD=DBの時、2DE=BCである。
ということになるのですが、分かりづらいですよね。
簡単に言います。
「三角形の底辺でない2つの辺の中点を結んでできた線は底辺に並行で、底辺の半分の長さになる」ということです。
もう一度図を見てもらえれば分かると思います。
ぜひ押さえておいてください!
面積・体積
相似な図形は、拡大と縮小の関係と言いました。
この時、相似比というものが出てきます。
要するに、どれくらい拡大や縮小をしたものなのかを表す値です。
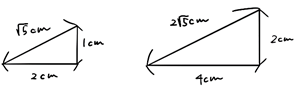
上の相似な三角形の相似比を求めてみましょう。
相似比は、対応する辺の長さを比較することで分かります。
底辺を比べると、2:4ですね。
相似比は基本的に、できるだけ簡単な数字にした方が分かりやすいので
2:4→1:2とします。
これが相似比です。
この相似比が分かれば、片方の面積を求めるだけで、両方の面積が分かるんです。
この時使うのが、面積比。
相似比の2乗の値で表されます。
上の三角形では、相似比が1:2なので1²:2²=1:4となります。
ぜひ、上の三角形で確かめてみてください。
この面積比を使う問題は、急にポンと出てくることが多いので覚えておきましょう。
すごく稀に、体積比というものが出てきます。
その時は、相似比の3乗です。
一応知識として言っておきます。
練習問題
それでは早速、練習問題を解いてみましょう!
(解答は下にあります。)
問題
(1)三角形の相似の条件を3つ答えよ。
(2)図を見て答えなさい。
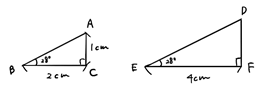
(a)DFの長さを求めよ。
(b)⊿DEFの面積を求めよ。
(3)図を見て答えなさい。
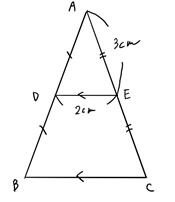
(a)BCの長さを求めよ。
(b)⊿ABCの面積は⊿ADEの何倍か。
解答
(1)の解答
・3つの辺の比がすべて等しい
・2つの角が等しい
・2組の辺の比とその間の角が等しい
(2)の解答
⊿ABCと⊿DEFの相似比は1:2なので、DFはACの2倍になります。
よって、DF=2です。
DFの長さが分かったので、底辺×高さをしてもいいですし、相似比を使って求めても良いと思います。
答えは、4
(3)の解答
中点連結定理から、BC=2DEなので、BC=4となる。
また、⊿ADEと⊿ABCの相似比は1:2なので、面積比は1:4となる。
よって、4倍である。
相似のまとめ
お疲れさまでした。相似は理解できたでしょうか。
他の単元もそうですが、相似は特に慣れが必要であると思います。
相似の条件を覚えて、瞬時に気づけるくらいにはしたいところですね。
慣れてきたら、他の問題も解いてみましょう。







